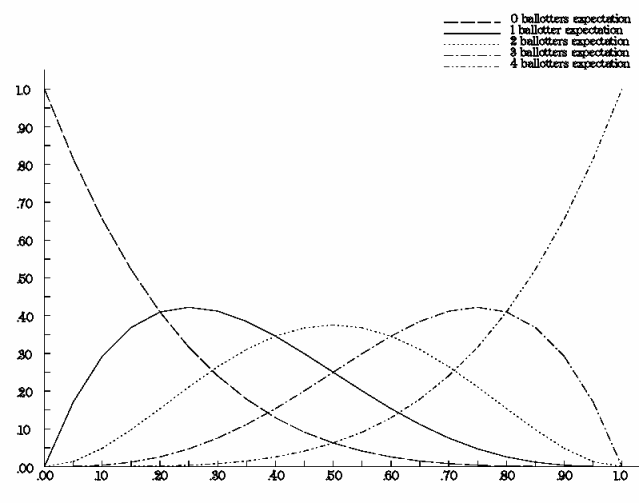

Each curve plots the expectation that a given number of individuals will end up balloting, over the full range (0..1) of participation probabilities. Note that to maximize the probability of exactly 1 ballotter, each individual ought to participate 25% of the time as seen by the maximum in the 1 ballotter curve at 0.25. Over-participation leads to maximizing greater numbers of ballotters. The probability of 3 ballotters, for instance is maximized with a 0.75 participation probability. Conversely, under-participation leads to near-zero numbers of ballotters. A 0.05 participation probability makes it very likely (about 80%) that 0 individuals will end up balloting in a given lottery.